Видеоинструкция, как сделать объемную цифру для фотозоны

Пожаловаться

Обновлено 28 янв 2020

День рождения — особенный праздник не только для детей, но и для их родителей. Где купить вкусный торт, во что нарядить имененника и, конечно, как оформить фотозону — вот вопросы, которые задают себе все мамы незадолго до важной даты. С последним наш журнал может помочь!

Читайте также:

Вишлист: 15 идей подарков малышу на первый день рождения

Мы нашли отличный способ, помогающий сделать объемную цифру для детского праздника всего за один вечер. С этой работой справится любая мама, а милый реквизит после праздника можно продать.

© Instagram @anna.klinova

Вам понадобится:

• линейка
• ручка
• кусок обоев
• ножницы
• двусторонний скотч
• пенопласт (толщиной 30-50 мм)
• салфетки
• степлер
• клей ПВА

Как сделать объемную цифру:

1. На ненужном куске обоев начертите цифру (все размеры вы найдете на картинке ниже), вырежьте. Дважды перенесите ее на пенопласт и вырежьте заготовки.

Кадр из видео

2. Наклейте двусторонний скотч по периметру одной из получившихся пенопластовых цифр. Уберите верхний бумажный слой и склейте заготовки между собой.

3. Сделайте цветы. Для этого дополнительно сверните салфетку вчетверо, закрепите середину степлером, по краям сделайте насечки с помощью ножниц. Распушите — и цветок готов. Их понадобится много, поэтому можно подключить к работе мужа или подругу.

Читайте также:

Мастер-класс: делаем кукольный домик своими руками

4. Постепенно нанося клей, прикрепите к пеносластовой заготовке цветы. Клейте их близко друг к другу, чтобы не просвечивался пенопласт.

5. Объемная цифра готова! При желании можно украсить ее бантиком.

Посмотрите это видео, в нем пошагово показан весь процесс создания:

Конечно, в этой технике можно делать не только цифры, но и буквы или силуэты животных. И не только для детских, но и для взрослых фотозон!

Читайте также:

• Без фанеры и гвоздей: как сделать детский ночник своими руками
• Час – и готово! 6 идей, как сделать коврик для любой комнаты
• Лучше, чем у принца Джорджа: интересные детские качалки

Фото на анонс: Instagram @alenax88, @olya_durneva_ph

28 марта 2019 18:23 | Отредактировано: 28 января 2020 22:51

Мастер-класс: вяжем модный клатч

В садик, в школу, на прогулку: подбираем термосы и ланчбоксы

Нет ничего особенно сложного, если разбить это на мелкие шаги. И у вас все обязательно получится!

Комментарии

Узнавай и участвуй

Клубы на Бэби.ру — это кладезь полезной информации

Буллинг: как помочь ребенкуНовогоднее чудо: никто не останется без праздникаКак сделать шрам после кесарева менее заметным?ТОП-25 Новогодних подарков для детей всех возрастовПомощь государства детям с диабетомТоп-10 девайсов для кормящей мамыОцените состояние иммунитета вашего ребенкаОнлайн приёмная психолога — для мам часто болеющих детейПочему ребенок часто болеет?

мастер класс с фото.

Как сделать цифру из салфеток. Пошаговый мастер-класс по изготовлению цифры 2 из салфетокBagiraClub Женский клуб

Оформление праздничного интерьера своими руками сегодня стало очень модным веянием. Можно сделать все что угодно: растяжки из букв и флажков, большие цифры, веселые колпачки для гостей и многое другое.  Такая атрибутика создает веселую атмосферу и прекрасно смотрится на фотографиях. Чаще всего украшения изготавливают на детские дни рождения. В данном мастер-классе я подробно расскажу и покажу вам, как сделать объемную цифру из салфеток.

Содержание

• Цифра из салфеток: материалы для изготовления
• Как сделать объемную цифру из салфеток
  • Делаем цветочки из салфеток
  • Мастерим каркас из картона
  • Собираем и украшаем цифру

Цифра из салфеток: материалы для изготовления

Цифра из салфеток является достаточно «бюджетным», но одновременно эффектным элементом праздничного декора. Основные материалы для ее изготовления – это плотный картон и обычные бумажные салфетки.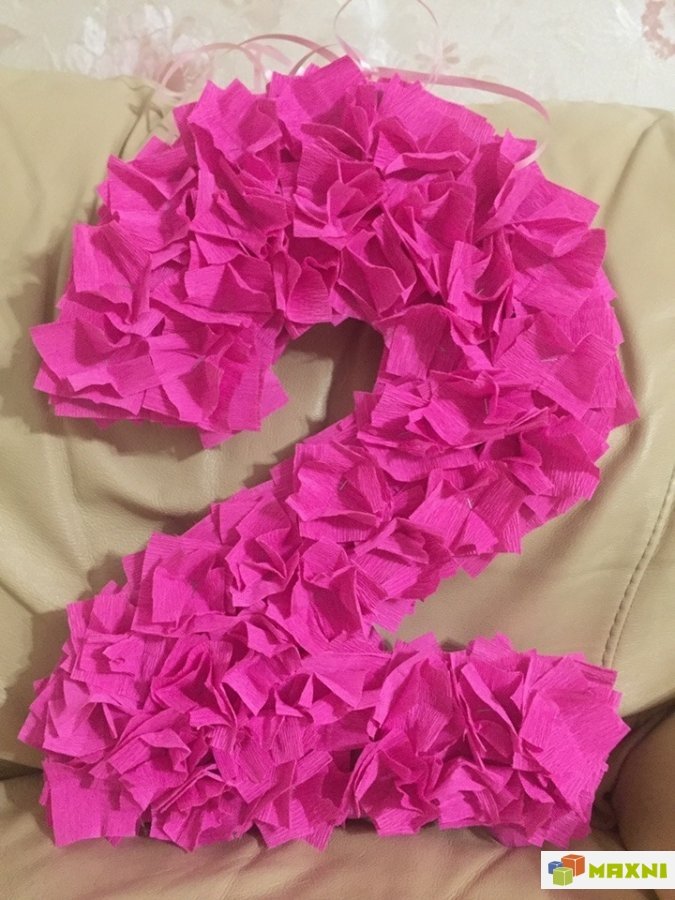

Для каркаса нам потребуются листы плотного упаковочного картона (гофрокартон), поэтому здесь пригодится старая ненужная коробка от бытовой техники. У меня нашлась коробка габаритами 50×30 см.

Салфетки – из них мы будем делать ажурные цветочки. Они бывают разного размера и количества в упаковке. Заранее предугадать, сколько их понадобится очень сложно, здесь нужно ориентироваться на размеры картона для будущей цифры. Но лучше всего взять одну-две упаковки про запас. Ведь в дальнейшем они пригодятся для оформления праздничного стола. Для своей цифры я приобрела 4 упаковки красных салфеток и одну – белых (по факту их понадобилось 2).

Также нам будут нужны вспомогательные материалы:

• Большие ножницы или строительный резак.
• Широкий скотч.
• Степлер и скобы для него.
• Клей момент универсальный.
• Лист картона «под золото» для украшения (у меня голографический).

Как сделать объемную цифру из салфеток

Для начала хочется отметить, что цифры из салфеток бывают плоские и объемные.

Плоские изделия делаются быстрее, так как не нужно клеить каркас, достаточно просто вырезать контур из листа картона. А также потребуется в разы меньше цветочков для ее украшения.

На объемную фигуру понадобится больше времени и материалов. Однако она оправдает потраченные усилия своим эффектным внешним видом.

В сегодняшнем мастер-классе я расскажу вам, как сделать объемную цифру «два». Весь процесс ее изготовления можно разделить на 3 этапа. Далее я подробно опишу каждый их них.

Делаем цветочки из салфеток

Данный этап очень простой, но занимает приличное количество времени, так как цветочков понадобится очень много. Если у вас есть помощники, то советую привлечь их к этому делу.

Я начала работу с салфеток красного цвета. Они двухслойные, а их размер в развернутом виде – 33 см, поэтому из одной салфеточки получается 2 цветочка.

Итак, цветок делается следующим образом:

1. Берем одну салфетку и разрезаем ее пополам.
2. Половинки складываем пополам еще раз и опять разрезаем.
3. Складываем вместе 2 четвертинки и скрепляем их в середине степлером.
4. Затем из квадратика вырезаем круг. Я делаю это «на глаз».
5. Далее пальцами сжимаем каждый слой по очереди, начиная с верха. Чтобы цветочек получился ажурнее и пышнее очень важно сильно сжать их в конце, как показано на фотографии.
6. Разворачиваем цветок, аккуратно расправляя лепестки. Вот, что получается в итоге.

Чтобы оптимизировать процесс, сначала я сделала много вот таких заготовок, из которых потом получились прекрасные цветы.

Белые цветочки мастерят по тому же принципу. Однако имеющиеся у меня белые салфетки, в отличие от красных, однослойные и меньше по размеру. Поэтому чтобы заготовки получились одного размера, мне пришлось приложить немного больше усилий:

1. Я складывала вместе 3 белые салфетки, а сверху на них прикладывала красный квадратик нужного размера и вырезала заготовку по его контуру.
2. Далее все делается по вышеописанной схеме, и в результате получается вот такой нежный цветочек.

Всего для оформления цифры мне потребовалось изготовить 86 красных и 65 белых цветочков. На это ушло примерно 4 часа.

Мастерим каркас из картона

Для того, чтобы соорудить объемный каркас мне понадобилось 2 листа гофрокартона размерами 50×30 см. Из них я вырезала лицевые части «двойки». Оставшиеся обрезки от коробки пошли на боковую часть цифры.

Порядок действий был таков:

1. Сначала на одном из листов я нарисовала контур цифры «два». Ширину его я определила, ориентируясь на количество рядов цветочков, которые можно будет на него наклеить. Еще одно условие – цифра при этом должна выглядеть пропорционально. Исходя из размеров моего картона, у меня получилось 2 рядка цветочков. Поэтому ширина цифры по всему периметру получилась 9 см.
2. Затем я вырезала «двойку». Так как картон оказался очень плотным и твердым, то я использовала строительный резак.
3. Получившуюся цифру я положила на второй лист картона, обвела ее по контуру и тоже вырезала.
4. Далее я сделала заготовки для боковой части изделия. Для этого я отмерила и вырезала из картона полоски шириной 9 см. Совет! Чем они длиннее, тем удобнее их будет приклеивать.
5. При помощи скотча, кусочками шириной примерно 10-12 см, склеиваем сначала одну половинку «двойки» с полосками для боковой части. Здесь же хочу отметить, что на бока я использовала картон, который был каркасом внутри коробки, а он оказался более мягким и гибким. Благодаря этому сгибать и клеить его по контуру «двойки» было легче. Промежуточные итоги видны на фото.
6. Аналогичным способом приклеиваем вторую часть «двойки». Вот, что в результате у меня получилось.

Собираем и украшаем цифру

Далее начинаем приклеивать цветочки на каркас. Для этого я использую универсальный клей-гель «Момент», так как он бесцветный и быстро схватывается.

Чтобы не помять цветы, я слегка надавливаю на них сверху, а затем аккуратно прижимаю пальцем их основание под лепестками.

Когда клей хорошенько высохнет, расправьте цветочки, чтобы они выглядели пышнее.

Дизайн циферки может быть любым, все зависит от вашей фантазии и цветовой гаммы салфеток.

Свою «двойку» я решила украсить короной. Чтобы упростить задачу, я нашла в Интернете готовый трафарет подходящих размеров, распечатала его и вырезала.

Так как цифра у меня двухсторонняя, то и корона должна быть такой же. Поэтому я обвела ее 2 раза на листе голографического картона формата А4.

Затем вырезала обе половинки и склеила их. В результате она получилась «золотой» с обеих сторон.

Заключительным этапом я торжественно «короновала» свою циферку, аккуратно приклеив ее к цветочкам. Готово!

По аналогичному принципу можно изготовить абсолютно любую цифру или даже букву.

трехмерных фигур | SkillsYouNeed

На этой странице рассматриваются свойства трехмерных или «твердых» форм.

Двумерная фигура имеет длину и ширину. Трехмерная твердая форма также имеет глубину. Трехмерные формы по своей природе имеют внутреннее и внешнее, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.

На этой странице рассматриваются как прямолинейные тела, называемые многогранниками, которые основаны на многоугольниках, так и тела с кривыми, такие как шары, цилиндры и конусы.

Многогранники

Многогранники (или многогранники) представляют собой твердые тела с прямыми сторонами. Многогранники основаны на многоугольниках, двумерных плоских формах с прямыми линиями.

См. нашу страницу Свойства полигонов, чтобы узнать больше о работе с полигонами.

Многогранники определяются как имеющие:

• Прямые ребра .
• Плоские стороны называются гранями .
• Углов, называемых вершинами .

Многогранники также часто определяются количеством ребер, граней и вершин, которые они имеют, а также тем, имеют ли их грани одинаковую форму и размер. Как и многоугольники, многогранники могут быть правильными (на основе правильных многоугольников) или неправильными (на основе неправильных многоугольников). Многогранники также могут быть вогнутыми или выпуклыми.

Одним из самых простых и привычных многогранников является куб. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.

Правильные многогранники (Платоновые тела)

Пять правильных многогранников представляют собой особый класс многогранников, все грани которых идентичны, причем каждая грань является правильным многоугольником. Платоновые тела:

• Тетраэдр с четырьмя равносторонними треугольными гранями.
• Куб с шестью квадратными гранями.
• Октаэдр с восемью равносторонними треугольными гранями.
• Додекаэдр с двенадцатью пятиугольными гранями.
• Икосаэдр с двадцатью равносторонними треугольными гранями.

См. рисунок выше для иллюстрации каждого из этих правильных многогранников.

Что такое призма?

Призма — это любой многогранник, который имеет два совпадающих конца и плоские стороны . Если вы разрежете призму в любом месте по ее длине, параллельно ее концу, ее поперечное сечение будет таким же — вы получите две призмы. Стороны призмы параллелограммов — четырехугольников с двумя парами сторон одинаковой длины.

Антипризмы аналогичны обычным призмам тем, что их концы совпадают. Однако стороны антипризмы состоят из треугольников, а не из параллелограммов. Антипризмы могут стать очень сложными.

Что такое пирамида?

Пирамида — это многогранник с многоугольниками в основании , который соединяется с вершиной (верхняя точка) с прямыми сторонами.

Хотя мы склонны думать о пирамидах с квадратным основанием, вроде тех, что строили древние египтяне, на самом деле они могут иметь основание любого многоугольника, правильного или неправильного. Кроме того, пирамида может иметь вершину прямо в центре основания, т.0019 Правая пирамида или может иметь вершину не по центру, если это  Наклонная пирамида .

Более сложные многогранники

Существует множество других типов многогранников: симметричные и асимметричные, вогнутые и выпуклые.

Архимедовы тела, например , состоят как минимум из двух различных правильных многоугольников.

Усеченный куб (как показано на рисунке) представляет собой архимедово тело с 14 гранями. Шесть граней представляют собой правильные восьмиугольники, а остальные восемь — правильные (равносторонние) треугольники. Фигура имеет 36 ребер и 24 вершины (угла).

Трехмерные фигуры с кривыми

Твердые фигуры с изогнутыми или круглыми краями не являются многогранниками. Многогранники могут иметь только прямые стороны. Также см. нашу страницу о двумерных изогнутых формах.

Многие объекты вокруг вас будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными искривленными телами являются цилиндры, конусы, сферы и торы (множественное число для тора).

Обычные трехмерные формы с кривыми:
Цилиндр	Конус
Цилиндр имеет одинаковое поперечное сечение от одного конца до другого. Цилиндры имеют два одинаковых конца либо круга, либо овала. Несмотря на то, что они похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами.	Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание.
Сфера	Тор
Сфера, имеющая форму шара или шара, представляет собой полностью круглый объект. Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы.	Правильный кольцевой тор, имеющий форму кольца, шины или бублика, образован вращением меньшего круга вокруг большего круга. Существуют и более сложные формы торов.

Площадь поверхности

На нашей странице, посвященной расчету площади, объясняется, как вычислить площадь двухмерных фигур, и вам необходимо понимать эти основы, чтобы вычислять площадь поверхности трехмерных фигур.

Для трехмерных фигур мы говорим о площади поверхности , чтобы избежать путаницы.

Вы можете использовать свои знания о площади двухмерных фигур для вычисления площади поверхности трехмерной фигуры, поскольку каждая грань или сторона фактически представляет собой двумерную форму.

Таким образом, вы вычисляете площадь каждой грани, а затем складываете их вместе.

Как и в случае с плоскими формами, площадь поверхности твердого тела выражается в квадратных единицах: см ² , дюймы ² , м ² и так далее. Вы можете найти более подробную информацию о единицах измерения на нашей странице Системы измерения .

Примеры расчета площади поверхности

Куб

Площадь поверхности куба равна площади одной грани (длина x ширина), умноженной на 6, поскольку все шесть граней одинаковы.

Поскольку грань куба представляет собой квадрат, вам нужно провести только одно измерение — длина и ширина квадрата по определению одинаковы.

Таким образом, одна грань этого куба равна 10 × 10 см = 100 см ² . Умножаем на 6 количество граней куба, и получаем, что площадь поверхности этого куба равна 600см ² .

Другие правильные многогранники

Точно так же можно вычислить площадь поверхности других правильных многогранников (платоновых тел), найдя площадь одной стороны и умножив результат на общее количество сторон — см. диаграмму основных многогранников выше. .

Если площадь одного пятиугольника, составляющего додекаэдр, равна 22см ² , то умножьте это на общее количество сторон (12), чтобы получить ответ 264см ² .

Пирамида

Чтобы вычислить площадь поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:

Сначала определите площадь основания (квадрата) длина × ширина.

Далее определите площадь одной стороны (треугольника). Измерьте ширину вдоль основания, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.

Есть два способа вычислить площадь поверхности четырех треугольников:

• Разделите ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножьте на 4, чтобы получить площадь поверхности всех четырех сторон, или

• Умножьте ответ на 2.

Наконец, сложите площадь основания и сторон, чтобы найти общую площадь поверхности пирамиды.

Для расчета площади поверхности других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (площадь боковых сторон). Возможно, вам придется измерить стороны по отдельности.

Диаграммы сетей

Геометрическая сеть представляет собой двухмерный «шаблон» для трехмерного объекта. Сети могут быть полезны при расчете площади поверхности трехмерного объекта. На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды, если пирамида «развернута», у вас остается сеть.

Для получения дополнительной информации о схемах сети см. нашу страницу 3D-формы и сети .

Призма

Для расчета площади поверхности призмы :

Призмы имеют два одинаковых конца и плоские стороны в виде параллелограмма.

Вычислите площадь одного конца и умножьте на 2.

Для правильной призмы (у которой все стороны одинаковы) вычислите площадь одной из сторон и умножьте на общее количество сторон.

Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.

Сложите два ответа вместе (концы + стороны), чтобы найти общую площадь поверхности призмы.

Цилиндр

Пример:
Радиус = 5 см
Высота = 10 см

Чтобы вычислить площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте себе банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги. Если вы отрежете сторону по длине и сгладите ее, у вас получится прямоугольник. Следовательно, вам нужно найти площадь двух кругов и прямоугольника.

Сначала определите площадь одного из кругов.

Площадь круга равна π (пи) × радиус ² .

При радиусе 5 см площадь одного из кругов равна 3,14 × 5 ² = 78,5 см ² .

Умножьте ответ на 2, так как кругов два 157см ²

Площадь стороны цилиндра равна периметру круга × высоте цилиндра.

Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4·9.0003

Измерьте высоту цилиндра. В данном примере высота составляет 10 см. Площадь стороны 31,4 × 10 = 314см ² .

Общая площадь поверхности может быть найдена путем суммирования площади кругов и стороны:

157 + 314 = 471 см ²

Пример:
Радиус = 5 см

Конус

При расчете площади поверхности конуса необходимо использовать длину «наклона», а также радиус основания.

Однако вычислить его относительно просто:

Площадь круга в основании конуса составляет π (пи) × радиус ² .

В этом примере расчет равен 3,14 × 5 ² = 3,14 × 25 = 78,5 см ²

Площадь стороны, наклонной части, можно найти по следующей формуле:

π (пи) × радиус × длина наклона.

В нашем примере расчет равен 3,14 × 5 × 10 = 157 см ² .

Наконец, добавьте площадь основания к площади стороны, чтобы получить общую площадь поверхности конуса.

78,5 + 157 = 235,5 см ²

теннисный мяч:
диаметр = 2,6 дюйма

сфера

4 × π × радиус ² .

Для сферы часто проще измерить диаметр — расстояние поперек сферы. Затем вы можете найти радиус, который составляет половину диаметра.

Диаметр стандартного теннисного мяча составляет 2,6 дюйма. Таким образом, радиус составляет 1,3 дюйма. Для формулы нам нужен радиус в квадрате. 1,3 × 1,3 = 1,69

Таким образом, площадь поверхности теннисного мяча равна:

4 × 3,14 × 1,69 = 21,2264 дюйма ² .

Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см

Тор

Чтобы вычислить площадь поверхности тора , вам нужно найти два значения радиуса.

Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.

Малый или малый радиус (r) измеряется от середины кольца до внешнего края.

На диаграмме показаны два вида примера тора и способы измерения его радиусов (или радиусов).

Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаков для каждой части.

Формула: площадь поверхности = (2πR)(2πr)

Чтобы вычислить площадь поверхности примера тора.

(2 × π × R) = (2 × 3,14 × 20) = 125,6

(2 × π × r) = (2 × 3,14 × 4) = 25,12

Перемножьте два ответа, чтобы найти общую поверхность площадь примерного тора.

125,6 × 25,12 = 3155,072 см ² .

Дальнейшее чтение из книги «Навыки, которые вам нужны»

Понимание геометрии
Часть руководства «Навыки, которые вам нужны» для счета

Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и тел. Эти концепции построены в книге, с примерами работы и возможностями для вас, чтобы попрактиковаться в ваших новых навыках.

Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас.

Заполнение твердого тела: объем

Для трехмерных фигур вам также может понадобиться знать объем объем у них есть.

Другими словами, если вы наполнили их водой или воздухом, сколько наполнения вам потребуется?

Это описано на нашей странице Расчет объема .

SCIRP Открытый доступ

Издательство научных исследований

Журналы от A до Z

Журналы по темам

• Биомедицинские и биологические науки.
• Бизнес и экономика
• Химия и материаловедение.
• Информатика. и общ.
• Науки о Земле и окружающей среде.
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные науки. и гуманитарные науки

Журналы по тематике  

• Биомедицина и науки о жизни
• Бизнес и экономика
• Химия и материаловедение
• Информатика и связь
• Науки о Земле и окружающей среде
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные и гуманитарные науки

Публикация у нас

• Подача статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Публикуйте у нас  

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Подпишитесь на SCIRP

Свяжитесь с нами

клиент@scirp. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт