Как сделать объемные цифры на день рождения: Объемные цифры на День Рождения: схемы, уроки
Объемные цифры своими руками на праздник
День рождение деток – праздник, который родители сначала ждут больше, чем сами именинники. Ведь процесс организации, подготовки подарков, декоративных элементов – всегда предоставляет приятные хлопоты. Невероятной атмосферы празднику преподнесут объемные цифры своими руками. Их изготовление займет немного времени, зато подарит море эмоций всем гостям торжества. Предлагаем рассмотреть несколько простых идей для создания такого аксессуара.
Содержание
- Как сделать объемную цифру из салфеток
- Объемные цифры своими руками из пенопласта
- Цифра на день рождения из гофрированной бумаги
Как сделать объемную цифру из салфеток
Изготовление праздничного декора – простой процесс, который требует минимум материальных средств, немного свободного времени. Подготовьте:
- картон;
- ножницы;
- салфетки желаемого цвета;
- нити;
- клей.
Первое, что нужно выполнить, это нарисовать нужный символ на картонном основании. При чем, сделайте это в двух вариантах – обычном и зеркальном, чтобы потом можно было скрепить изделие, сформировав объемный знак.
При чем, сделайте это в двух вариантах – обычном и зеркальном, чтобы потом можно было скрепить изделие, сформировав объемный знак.
Процесс создания
Когда все детали знаков будут соединены, приступайте к их отделке. Девочкам отлично подойдут цифры на день рождения в виде цветочков. Делаем их по такому принципу:
- берем салфетки, складываем гармошкой;
- середину заматываем нитками, чтобы сформировался бант;
- лепестки расправляем к центру, передвигаясь к краям, в середине формируем бутон, плотно прижимая бумагу.
Теперь салфетки складываем в большую стопку, вырезаем лепесточки. Розу разворачиваем, чтобы сдвинулись лепесточки, кончик соединяем с углом. Цветок делаем объемным, приклеиваем на картонное основание. Затем повторяем действия, формируя еще несколько цветков, заполняя весь картонный макет по периметру.
Цветочная тройка
Если цифры из салфеток с цветочками сложно формировать, тогда можете скрутить трубочки из бумажного материала, а затем им украсить конструкции, как показано на фото:
Трубочки для циферки
Объемные цифры своими руками из пенопласта
Чтобы получилась красивая праздничная конструкция, воспользуйтесь такими материалами:
- листовым пенопластом;
- гофрированной бумагой или салфетками;
- канцелярским ножом;
- ножницами;
- степлером;
- клеевым пистолетом;
- скотчем.

Обычно для работы применяется пенопласт, который используется в термоизоляции. Выбирайте диаметр, в зависимости от желаемой толщины конструкции. Затем воспользуйтесь таким мастер-классом:
- Нанесите цифровой макет на основании из пенопласта, скрепите их скотчем.
- Затем салфетка складывается на 2 части, разрезается, чтобы сформировался квадрат из 2 слоев. Полученный квадрат складывается еще 2 раза, затем скрепляется степлером со вторым фрагментом.
- Многослойные квадратики преобразуются ножницами, распушиваются.
- Цветки крепятся на основании из пенопласта, для этого используйте клей-пистолет. Обязательно каждый цветочек промазывается клеем.
- Украшайте конструкцию с обеих сторон, приклеивая декоративные фрагменты, максимально близко друг к другу.
При увлеченной работе удастся сформировать креативную цифру всего за 2-3 часа.
Объемная цифра из пенопласта
Цифра на день рождения из гофрированной бумаги
Интересные объемные цифры своими руками получаются из гофрированной бумаги. Они тоже изготавливаются достаточно просто, детальный мастер-класс можно посмотреть на видео:
Они тоже изготавливаются достаточно просто, детальный мастер-класс можно посмотреть на видео:
Объемные Цифры из Пенопласта на заказ от 70 руб/шт
Объемные цифры из пенопласта – красивый декор
Объемные цифры из пенопласта – сравнительно недорогой, но действенный способ привлечь внимание клиентов к вашему товару, украсить территорию торгового центра, проинформировав о предстоящих акциях (например, «-20% на все!») или удивить гостей необычным декором помещения.
Компания «Русский Пенопласт» работает в сфере изготовления оригинальных изделий из пенополистирола с 2013 года и заслужила репутацию надежного партнера. Мы гарантируем клиентам быстрое, в течение 2-48 часов, и качественное выполнение проекта любой сложности.
Постоянные и новые клиенты уже оценили преимущества сотрудничества с нашей компанией:
|
|
|
|
|
|
|
Применение объемных цифр из пенопласта
Подобный яркий и необычный декор с успехом используется при проведении:
|
Выставок
|
|
|
|
|
|
|
|
Фотосессий |
|
|
Купить объемные цифры из пенопласта – значит получить возможность дешево, но при этом эксклюзивно, оформить торжество, украсить помещение, привлечь покупателей нестандартной рекламой. Красочные изделия в матовых или глянцевых тонах «приковывают» взгляды прохожих, гостей, потенциальных заказчиков.
|
|
|
|
Специалисты компании «Русский Пенопласт» спроектируют и изготовят объемные цифры из пенопласта в срок от 2 часов до 2-3 дней.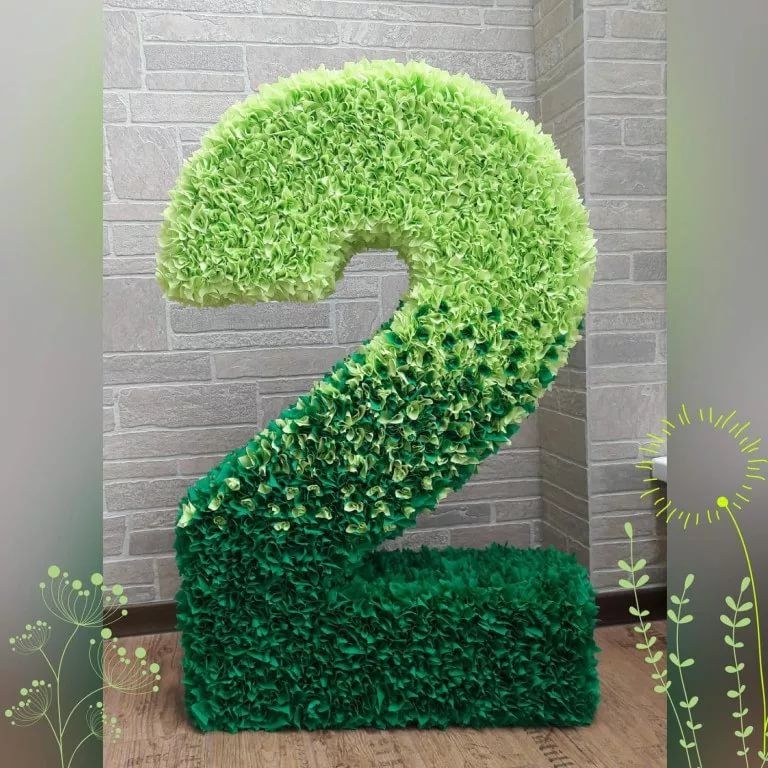 Собственное производство и современное оборудование обеспечивают изготовление конструкций под заказ по лучшим ценам в Москве и Московской области.
Собственное производство и современное оборудование обеспечивают изготовление конструкций под заказ по лучшим ценам в Москве и Московской области.
Стоимость объемных цифр из пенополистирола
Цена пенопластовых цифр, по сравнению с аналогами из металла или пластика, в 2-3 раза ниже, при этом эксплуатационные качества конструкций не уступают изделиям из других материалов. К тому же, пенопласт очень легкий, удобный для транспортировки, быстро монтируется на клей или двухсторонний скотч.
|
ВЫСОТА ЦИФРЫ, СМ |
ТОЛЩИНА ПЕНОПЛАСТА, СМ | |||||||
|---|---|---|---|---|---|---|---|---|
|
|
2 см |
3 см |
5 см |
10 см |
20 см |
30 см |
40 см |
50 см |
|
10 см |
70p |
90p |
110p |
170p |
340p |
510p |
680p |
850p |
|
15 см |
120p |
130p |
170p |
220p |
440p |
660p |
880p |
1100p |
|
20 см |
150p |
160p |
220p |
290p |
580p |
870p |
1160p |
1450p |
|
30 см |
240p |
260p |
310p |
410p |
820p |
1230p |
1640p |
2050p |
|
40 см |
330p |
360p |
410p |
530p |
1060p |
1590p |
2120p |
2650p |
|
50 см |
400p |
450p |
550p |
650p |
1300p |
1950p |
2600p |
3250p |
|
60 см |
490p |
550p |
670p |
830p |
1660p |
2490p |
3320p |
4150p |
|
70 см |
680p |
720p |
840p |
1010p |
2020p |
3030p |
4040p |
5050p |
|
80 см |
760p |
820p |
930p |
1210p |
2420p |
3630p |
4840p |
6050p |
|
90 см |
900p |
970p |
1120p |
1280p |
2560p |
3840p |
5120p |
6400p |
|
100 см |
970p |
1010p |
1210p |
1370p |
2740p |
4110p |
5480p |
6850p |
Воспользуйтесь формой на сайте «Заказать расчет» и в течение 30 минут узнаете стоимость изготовления пенопластовых объемных цифр по вашим рисункам, чертежам или фото.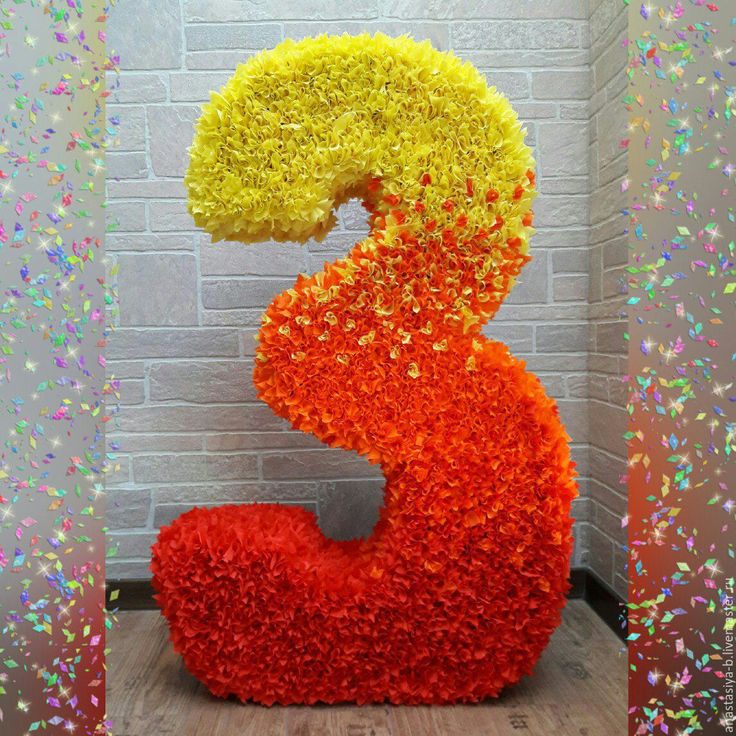
Резка конструкций осуществляется мастерами с 20-летним опытом на высокотехнологичном оборудовании – станках «Супер Макси». Благодаря этому все изделия прорабатываются до мельчайших деталей, отличаются первоклассным качеством и уникальным дизайном.
Стоимость объемных цифр из пенопласта на 10% ниже среднерыночной по Москве и области. Мы добились этого за счет уникальных схем управления производственными процессами и технологиями изготовления.
Дополнительное оформление пенопластовых цифр
У нас предусмотрен красивый декор для объемных цифр из пенопласта, который включает в себя:
|
|
| |
|
|
|
|
|
|
|
|
По желанию клиента обработаем изделия фасадными полимерными шпаклевками, антивандальным раствором. Чтобы усилить конструкцию, используем металлокаркас или армированную сетку.
Предусмотрена срочная резка объемных цифр из пенопласта в день поступления заказа. Учитываем все пожелания клиента и выполняем проекты, которые оказались не под силу другим компаниям.
Также в компании «Русский Пенопласт» организована доставка объемных цифр из пенополистирола по Москве, Московской области, всей России и СНГ. Предусмотрен самовывоз товара со склада в столице, расположенного по адресу: улица 1-ая Стекольная, дом 7, строение 7.
Сделать заказ на изготовление объемных цифр можно, обратившись к нам удобным способом:
|
|
|
|
|
|
|
|
|
|
|
|
Объем – формула, определение, расчет, примеры
Объем – это мера емкости, которую держит объект. Например, если чашка может вместить до краев 100 мл воды, говорят, что ее объем равен 100 мл. Объем также можно определить как объем пространства, занимаемый трехмерным объектом. Объем твердого тела, такого как куб или прямоугольный параллелепипед, измеряется путем подсчета количества содержащихся в нем единичных кубов. Лучший способ визуализировать объем — думать о нем с точки зрения пространства, заключенного/занятого любым трехмерным объектом или твердой формой. В этом можно убедиться с помощью простого упражнения дома:
- Возьмите прямоугольный лист бумаги длиной ‘ l ‘ см и шириной ‘ h ‘ см.
- Соедините противоположные стороны листа бумаги, не сгибая лист.
- Вы создали трехмерный объект, который заключает в себе пространство, из двухмерного листа.
1.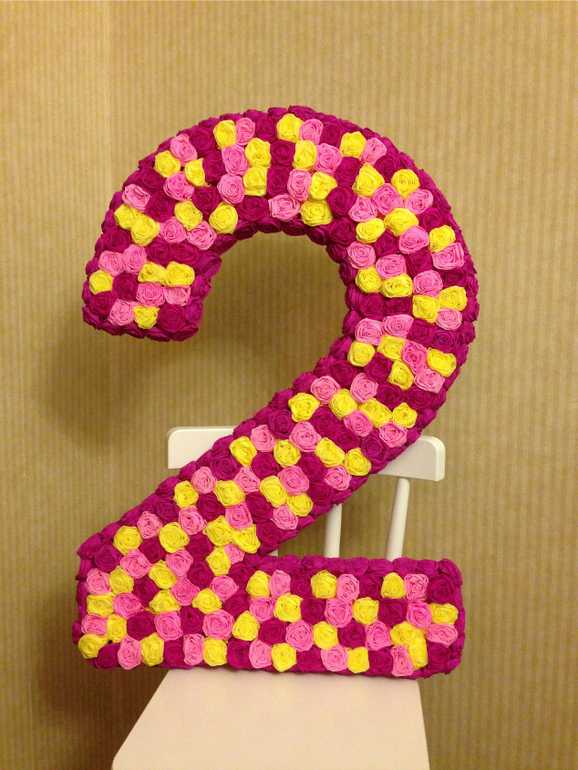 | Определение тома |
| 2. | Объем трехмерных фигур |
| 3. | Список формул объема |
| 4. | Как рассчитать объем? |
| 5. | Единицы объема |
| 6. | Калькулятор объема |
| 7. | Часто задаваемые вопросы о томе |
Определение тома
Объем определяется как объем, занимаемый трехмерной твердой формой. В любой форме это трудно визуализировать, но можно сравнить между формами. Например, объем ящика компаса больше объема помещенного в него ластика. Для вычисления площади любой двумерной фигуры мы делим часть на равные квадратные единицы. Точно так же при вычислении объема объемных фигур мы будем делить его на равные кубические единицы. Давайте узнаем, как рассчитать объем различных твердых фигур в нашем следующем разделе.
Объем 3D-фигур
Каждый объект в нашем окружении имеет свойство занимать пространство. Эти реальные объекты можно легко сравнить с основными трехмерными формами. Давайте посмотрим на объем этих твердых фигур в деталях.
Эти реальные объекты можно легко сравнить с основными трехмерными формами. Давайте посмотрим на объем этих твердых фигур в деталях.
Объем кубоида
Предположим, у нас есть несколько прямоугольных листов длиной ‘l’ и шириной ‘ b’ . Если мы сложим их один поверх другого до высоты ‘h’ , мы получим прямоугольный параллелепипед размерности л, б, з . Это можно увидеть на следующем рисунке, на котором показаны длина, ширина (ширина) и высота образованного таким образом прямоугольного параллелепипеда.
Чтобы вычислить объем пространства, заключенного в этот прямоугольный параллелепипед, мы используем формулу: Объем прямоугольного параллелепипеда = l × b × h
Объем кубоида
Куб является частным случаем прямоугольного параллелепипеда, где все три стороны равны по мере. Если мы представим это равное значение как «а», то объем этого куба можно будет рассчитать по формуле: Объем куба = а × а × а = а³. Обратите внимание на следующий рисунок, чтобы увидеть равные стороны куба и пространство, которое он занимает.
Обратите внимание на следующий рисунок, чтобы увидеть равные стороны куба и пространство, которое он занимает.
Объем цилиндра
Точно так же, как мы построили прямоугольный параллелепипед из прямоугольников, мы можем построить цилиндр из кругов того же размера.
Цилиндр представляет собой трубчатую структуру с двумя параллельными круглыми основаниями, которые соединены изогнутой поверхностью на фиксированном расстоянии от центра. Расстояние между этими двумя основаниями и есть высота цилиндра. Если мы рассмотрим «r» как радиус круглого основания (и вершины), а «h» как высоту цилиндра, то объем цилиндра можно выразить как объем цилиндра = π r² h
Объем пирамиды
Пирамиды имеют многоугольник в качестве основания и треугольные грани, которые сходятся на вершине. Объем пирамиды рассчитывается по формуле: Объем пирамиды = 1/3 × длина основания × ширина основания × высота пирамиды. Эту формулу также можно записать в виде 1/3 × площадь основания многоугольника × высота пирамиды.
Объем конуса
Разница между конусом и пирамидой в том, что основание конуса круглое, а основание пирамиды многоугольник. Объем конуса рассчитывается по формуле: 1/3 × πr 2 ч.
Объем шара
Объем шара – это занимаемое им пространство.
Объем сферы, радиус которой r равен 4/3 πr³.
Теперь, когда мы знакомы с формулами различных геометрических фигур, давайте взглянем на различные единицы объема.
Список формул объема
Ниже приведен подробный табличный список формул объема в двух словах, описывающий формулы объема для всех возможных трехмерных (твердых) форм.
Как рассчитать объем?
Вот шаги для расчета объема любой твердой формы:
- Определите все заданные параметры, которые являются полезными и которые необходимо заменить в соответствующей формуле объема. Например, радиус должен быть «r», а высота — «h», наклонная высота, диаметр и т.
 д.
д. - Убедитесь, что все параметры имеют одинаковые единицы измерения.
- Подставьте значения в формулу объема соответствующих форм.
- Запишите единицы измерения в кубических единицах.
Давайте разберемся с шагами на примере.
Пример: Найдите объем прямоугольного цилиндра радиусом 25 м и высотой 1 метр. Используйте π = 3,142.
Решение:
Радиус цилиндра равен r = 25 м.
Его высота h = 1 метр.
Объем цилиндра V = πr 2 h = (3,142)(25) 2 (1) = 1963,75 м 3 .
Объем баллона 1963,75 куб.м.
Единицы объема
Единицей объема в системе СИ является кубический метр (м 3 ), поскольку объем представляет собой количество трехмерного пространства, занимаемого формой или поверхностью. Однако наиболее часто используемой единицей измерения объема является литр. Кроме того, большие и малые объемы измеряются в других единицах, таких как миллилитры (мл), пинты, галлоны и другие. В следующей таблице показаны несколько единиц, связанных с объемом, и их метрические эквиваленты.
В следующей таблице показаны несколько единиц, связанных с объемом, и их метрические эквиваленты.
| Боковой блок | Единица объема | Метрический эквивалент |
|---|---|---|
| Дюйм | кубических дюймов (в 3 ) | 1 куб. дюйм = 16,387064 мл |
| Ножка | кубических футов ( 3 футов) | 1 куб.фут = 28,316846592 л |
| см | Кубический сантиметр (см 3 ) | 1 кубический сантиметр = 1 мл |
| Двор | Кубический ярд (ярд 3 ) | 1 куб. ярд = 764,554857984 л 1 куб.ярд = 0,764554857984 м 3 |
Хотя стандартной единицей измерения в США является кубический ярд или кубический дюйм, более широко используемыми единицами измерения являются галлоны, пинты или жидкие унции. В следующей таблице показаны некоторые из этих единиц и их эквивалентные метрические преобразования.
| Блок | Эквивалентное преобразование |
|---|---|
| 1 пинта (pt) | 2 чашки |
| 1 кварта (кварта) | 2 точки |
| 1 галлон (гал) | 3,78 литра |
| 1 литр | 1000 кубических сантиметров |
Калькулятор объема
Калькулятор объема помогает быстро и легко рассчитать объем любой заданной формы. Объем — это раздел математики, который занимается измерением емкости различных твердых тел. Попробуйте калькулятор объемов Cuemath прямо сейчас. Это онлайн-инструмент для простых и быстрых расчетов.
☛Также проверьте:
- Калькулятор объема цилиндра
- Калькулятор объема сферы
- Калькулятор объема куба
- Калькулятор объема прямоугольного параллелепипеда
☛Статьи по теме
Ознакомьтесь со статьями, посвященными объему различных объемных форм.
- Объем конуса
- Объем цилиндра
- Объем кубоида
- Том Пирамиды
Примеры томов
Пример 1: У Эдвина есть конический сосуд радиусом 6 дюймов и высотой 7 дюймов. Каков объем сосуда? Используйте π = 22/7.
Раствор.
Сосуд имеет форму конуса.
Объем конуса = 1/3 π r² h = 1/3 × 22/7 × 6 × 6 × 7 = 264 дюйма³
∴ Объем судна 264 куб. дюймПример 2: Джо любит играть со строительными блоками. Он построил конструкцию из 15 кубов. Если длина (ребро) каждого куба равна 3 дюймам, каков будет объем его конструкции?
Раствор.
Рассчитаем объем одного куба. Объем куба = ребро × ребро × ребро = 3 × 3 × 3 = 27 дюймов³
В его структуре 15 кубиков. Итак, объем всей конструкции:
Объем конструкции = 15 × объем одного куба = 15 × 27 = 405 дюймов³
∴ Объем конструкции 405 дюймов³.
Пример 3: Если диаметр мяча составляет 14 дюймов, сколько воздуха может вместить мяч? Используйте π = 3,14
Решение.
Количество воздуха внутри шара займет все пространство в шаре. Итак, нам нужно найти объем шара.
Радиус шара 14/2 дюйма = 7 дюймов
Объем шара = 4/3 πr³
= [4/3 × 3,14 × (7)³]
= 1436,02 дюйма³
∴ Мяч содержит 1436,02 дюйма³ воздуха.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.0003
Часто задаваемые вопросы по тому
Что означает объем?
Объем — это мера емкости, которую содержит объект. Скажем, если чашка может вместить 1000 мл сока, говорят, что ее объем равен 1000 мл. В этом случае объем также можно определить как количество сока, занимаемое чашкой. Объем всегда рассчитывается путем деления емкости фигур на равные кубические единицы.
В этом случае объем также можно определить как количество сока, занимаемое чашкой. Объем всегда рассчитывается путем деления емкости фигур на равные кубические единицы.
☛Загрузите прямо сейчас, чтобы попрактиковаться.
- Объем Рабочие листы
- Объем кубов Рабочие листы
- Объем конуса Рабочие листы
- Объем цилиндра Рабочие листы
Какова формула объема частичного конуса?
Объем частичного конуса можно рассчитать по формуле: V = 1/3 × πh(R² + Rr + r²), где «R» — радиус основания конуса, а «r» — радиус верхней поверхности.
☛ Прочтите основы здесь:
- Объем правого кругового конуса
- Объем частичного конуса
- Объем конуса в единицах числа Пи
Как найти объем пирамид?
Объем пирамиды рассчитывается по формуле: V = 1/3 × Площадь основания × Высота.
☛ Также проверьте:
- Объем прямоугольной пирамиды
- Объем треугольной пирамиды
- Объем прямоугольной пирамиды
Как найти объем конуса?
Объем конуса составляет 1/3 объема цилиндра той же высоты и такого же основания. Формула, используемая для нахождения объема конуса: 1/3 × π r² h; где «r» — радиус, а «h» — высота конуса.
Формула, используемая для нахождения объема конуса: 1/3 × π r² h; где «r» — радиус, а «h» — высота конуса.
Как найти объем цилиндра?
Объем цилиндра рассчитывается по формуле: V = площадь основания цилиндра × высота, а также представляется как объем цилиндра = π r² h; где «r» — радиус цилиндра, а «h» — высота.
В чем разница между объемом и площадью?
Объем фигуры или твердого тела — это пространство, занимаемое им, которое также включает его высоту или глубину. Измеряется в кубических единицах. Площадь – это пространство, занимаемое поверхностью плоской формы. Измеряется в квадратных единицах.
☛ Проверьте список важных математических формул:
- Формулы площади
- Формулы площади поверхности
- Геометрические формулы
- Формулы измерения
Каков объем мяча?
Поскольку шар является сферой, его объем будет рассчитан по формуле объема сферы. Формула объема сферы: 4/3 πr³, где «r» — радиус сферы.
Какая формула объема цилиндра?
Формула объема цилиндра = πr²h; где «r» — радиус основания цилиндра, а «h» — высота.
Как найти объем призмы?
Мы можем найти объем призмы, записав заданные размеры призмы. Затем подставьте значения в формулу объема V = B × H, где «V», «B» и «H» — это объем, площадь основания и высота призмы. Получив значение объема призмы, в конце запишите единицу объема призмы (в кубических единицах).
☛Чек:
- Объем призмы
- Объем призм. Рабочие листы
Как найти объем бака?
Объем резервуара зависит от его формы. В зависимости от размера мы можем использовать приведенные ниже формулы:
- Объем параллелепипеда = l × b × h; где «l» — длина прямоугольного параллелепипеда, «b» — ширина (ширина) прямоугольного параллелепипеда, а «h» — высота прямоугольного параллелепипеда.
- Объем куба = a 3 , где «a» — ребро куба.
- Объем цилиндра = π r 2 ч; где «r» — радиус основания цилиндра, а «h» — высота цилиндра.

- Объем конуса = 1/3 π r² h, здесь «r» — радиус круглого основания конуса, а «h» — высота конуса.
- Объем сферы = 4/3 πr³, где «r» — радиус сферы.
Калькулятор объема | PI Day
Сфера
Радиус
Том
Цилиндр
Радиус
Высота
Том
Том
CONE
RADIUS
0002 Высота
Объем
Прямоугольный параллелепипед
Длина
Высота
Объем
Вернуться на страницу калькуляторов
Калькулятор объема определит объем наиболее распространенных геометрических тел.
Что такое объем?
Объем — это общее пространство внутри твердого тела. Зная определение объема, мы можем теперь сосредоточиться на формулах объема обычных геометрических тел. Использовать эти формулы вручную не составит труда, но для получения быстрых и точных результатов каждый раз используйте калькулятор объема. 9{3}\), где r — радиус.
Просто введите размеры в калькулятор, чтобы найти объем. Единицы объема всегда будут кубическими, по сравнению с квадратными единицами площади поверхности.
@mometrixНужен калькулятор объема? Ссылка в био. ##pi ##piday ##volume ##sphere ##math ##mathhelp ##mometrix ##fyp
♬ оригинальный звук – Подготовка к тесту Mometrix
Вычисление объема куба Пример
Вот пример для расчет объема куба. 9{2}(4)=12\pi\) кубических сантиметров
Можно задаться вопросом, где этот калькулятор может быть полезен в реальных условиях. Это очень важно с точки зрения архитектуры и строительства. Одним из таких примеров является строительство дорог или тротуаров, где необходимо соорудить бетонные плиты. Как правило, бетонные плиты представляют собой прямоугольные тела, поэтому можно использовать калькулятор прямоугольной призмы.


 Заказать пенопластовые конструкции можно не только для оформления помещения, но и для уличной рекламы. Посетители однозначно не пройдут мимо красивых, тематически украшенных, объемных цифр из пенополистирола.
Заказать пенопластовые конструкции можно не только для оформления помещения, но и для уличной рекламы. Посетители однозначно не пройдут мимо красивых, тематически украшенных, объемных цифр из пенополистирола.

 Палитра RAL насчитывает 1625 оттенков.
Палитра RAL насчитывает 1625 оттенков.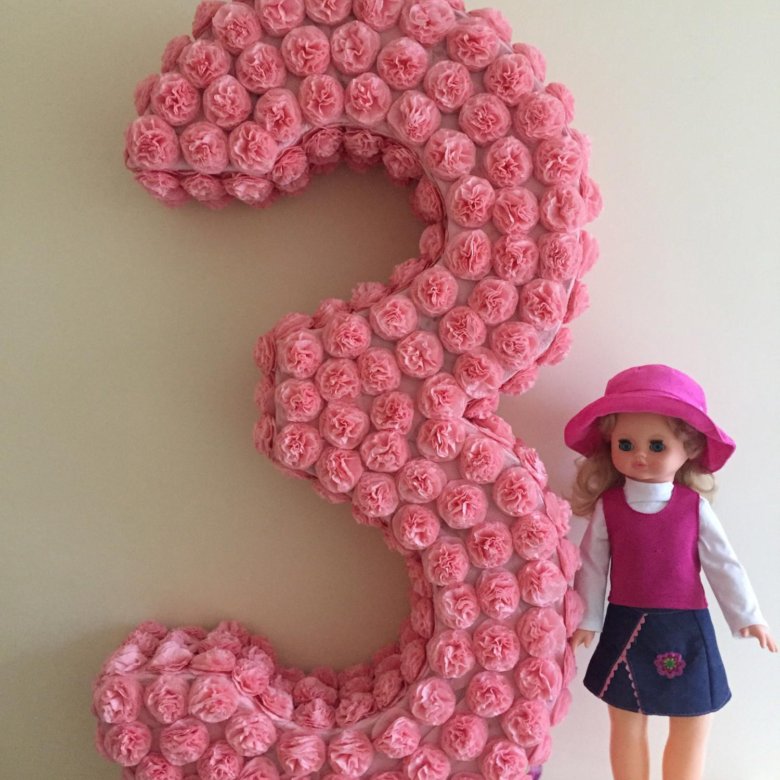
 д.
д.
