Цифра из картона: делаем пошагово своими руками

Цифры очень часто требуются на различных праздниках. Чаще всего – это Дни рождения, но это могут быть и другие праздники, связанные с определённой датой, например, 8 марта, 23 февраля. Мы расскажем вам, как сделать цифры из картонных коробок. Героиней нашей статьи будет цифра из картона.

Украшать помещения для праздника намного интереснее самостоятельно, чем позвать профессиональных декораторов. Пусть они могут сделать лучше, но в помещении, украшенном своими руками, находится куда приятнее.

Мастерим цифру из картона: список обязательных материалов и инструментов

Для того, чтобы сделать цифру из картона нам обязательно потребуются следующие инструменты и материалы:

• Ножницы
• Канцелярский нож
• Линейка
• Простой карандаш
• Картон
• Элементы декорирования

Со всеми материалами всё понятно, кроме последнего. Мы будем делать пошагово и элементы декорирования будут использоваться на последней стадии. Под элементами декорирования подразумевается то, чем будет украшен наш картонный каркас. Это могут быть салфетки, нитки, краски и множество других элементов, использовать которые у вас хватит фантазии.

Красивая тройка, украшенная салфетками:

Такая цифра будет очень красивым украшением на дне рождения девочки.

Давайте приступим к созданию данного творения. На фотографии изображена трёхмерная «версия» цифры – более сложная, есть простая – двухмерная. Начнём с более простой. Но сначала необходимо понять различие между ними. Двухмерная будет хорошо смотреться только на стенах. У неё красивый рисунок будет с одной стороны. А трёхмерная будет иметь объём и, если мы повернём её задом, она также будет иметь рисунок.

Для того что бы сделать двухмерную тройку нам, прежде всего, необходимо найти картон. Можно использовать картонную коробку. Разворачиваем её и получаем из её сторон прямоугольники. На одном из прямоугольников, который подходит по размерам, рисуем цифру три. Вырезаем её. Теперь необходимо её украсить салфетками. Можно сделать из них красивые цветочки или, разрезав салфетку на полоски, свернуть в трубочки. Наклеиваем трубочки на нашу картонную основу. Цифра готова!

Пробуем сделать поделку в 3D – очень красиво и креативно

Для изготовления трёхмерной цифры нам потребуется больше картона. Сначала вырезаем две одинаковые 2д тройки. Именно одинаковые! Они должны максимально совпадать по размерам. Если погрешности будут более двух миллиметров, то конечная цифра будет не такой красивой. Именно эти две заготовки будут основаниями нашей объёмной модели.

После того, как вы вырезали основания, вам необходимо сделать боковые грани. Но сначала определитесь с толщиной цифры. Наибольшую сложность для вырезания представляют скруглённые части. Есть два способа правильно подобрать длину. Первый заключается в использовании сантиметровой ленты, а второй в геометрических расчётах. Первый можно провести после того, как цифра уже вырезана, второй же, только во время черчения цифры.

По первому способу трудностей возникнуть не должно. Всё что вы должны сделать – это приложить ленту по дуге и измерить её длину.

Геометрический способ сложнее и не может быть использован в том случае, если вы сделали дугу не циркулем! Ищете точку на картоне, в которой находилась ножка циркуля, когда вы проводили дугу у тройки. Измеряем расстояние от данной точки до внутренней дуги. Это будет радиус. Далее делаем по этой формуле.

Всего у вас должно получиться девять частей: два основания и семь боковых деталей. Склеиваем их скотчем. Лучшего всего использовать именно скотч. Им намного проще выполнить данную задачу, чем клеем. Склеить элементы значительно сложнее, чем соединить скотчем.

И вот наш каркас готов. Теперь мы должны украсить его. Здесь можно использовать красные салфетки, что изображены на фотографии или можно использовать нитки. Вот пример цифры, украшенной нитками.

Первый случай хорошо подойдёт для девочки, а второй – для мальчика. В первом случае мы нам потребуется достаточно много салфеток. Сразу берём две-три упаковки. Можем сделать из них цветочки, а можем свернуть в трубочки, как в описании к двухмерной цифре.

Во втором случае мы должны обмотать цифру нитками. Не жалейте нитей и берите с большим запасом. Например, для двойки, нам потребовалось около десяти метров. Старайтесь покрыть каркас ровным слоем. Также следим за тем, чтобы соседние нити наматывались параллельно. Тут есть очевидное правило: чем больше каркас, тем больше времени потребуется на его обмотку. Но правило не работает по какой-то формуле. Если вы делаете цифру в два раза больше, вам потребует в четыре раза больше времени.

На этом наш мастер класс по изготовлению цифры из картона своими руками можно объявить закрытым. Спасибо за внимание!

Видео, посвященные теме статьи

Объемные цифры в категории «Свадебные товары»

Большие настенные 3Д часы дизайнерские 3D DIY Clock часы 003B (Римские цифры Черные) 70-150см

На складе в г. Одесса

Доставка по Украине

609 грн

409 грн

Купить

Интернет-магазин «Сityshark»

Настенные большие часы 3D с объемными цифрами от 60 до 120 см. BST 0301380

Доставка по Украине

447 — 499 грн

от 2 продавцов

447 грн

Купить

Happy Boom

Настенные часы 3D большие с объемными цифрами от 60 до 120 см. BST 0301374

Доставка по Украине

447 — 499 грн

от 2 продавцов

447 грн

Купить

Happy Boom

Настенные часы 3D большие с объемными цифрами от 60 до 120 см. BST 0301376

Доставка по Украине

447 — 499 грн

от 2 продавцов

447 грн

Купить

Happy Boom

Настенные часы 3D большие с объемными цифрами от 60 до 120 см. BST 0301382

Доставка по Украине

447 — 499 грн

от 2 продавцов

447 грн

Купить

Happy Boom

Настенные часы 3D с объемными цифрами от 60 до 120 см. BST 0301378

Доставка по Украине

447 — 499 грн

от 2 продавцов

447 грн

Купить

Happy Boom

Набор для изучения цифр 0-9. Объемные деревянные цифры, деревянные вкладыши с цифрами

На складе в г. Днепр

Доставка по Украине

150 грн

Купить

Just U — handmade studio

Часы 3d объемные разборные с цифрами и словами серебро до 1м

На складе в г. Киев

Доставка по Украине

565 грн

Купить

Landis

Часы 3d объемные разборные с цифрами и словами черные до 1м

На складе в г. Киев

Доставка по Украине

565 грн

Купить

Landis

Кольцо серебряное объемное Цифра 11,колечко оригинальной формы, регулируемый размер 16-17,5, серебро 925 пробы

Доставка из г. Одесса

462 грн

Купить

Silver Stone — серебро и натуральные камни

Наклейка объемная пластиковая ООПТ Цифры 24х10см арт.Y-L038

На складе

Доставка по Украине

22 грн

Купить

Магазин для всей семьи

Цифры объемные настольные из дерева

Доставка по Украине

80 грн

Купить

ТОВ «ТРАДИЦІЯ МАЙСТРА»

Часы 3d объемные разборные с римск цифрами серебро до 1м

На складе в г. Киев

Доставка по Украине

565 грн

Купить

Landis

Часы 3d объемные разборные со слов и цифр черные до 1м

На складе в г. Киев

Доставка по Украине

565 грн

Купить

Landis

Часы 3d светящиеся в темноте объемные разборные с 4 цифрами и штрихами до 1м

На складе в г. Киев

Доставка по Украине

772 грн

Купить

Landis

Смотрите также

Настенные объемные 3D часы разборные с цифрами и словами цвет серебро diy сделай сам Art Clock 3d зеркальные

На складе в г. Киев

Доставка по Украине

528 грн

Купить

Langeron

Настенные объемные 3D часы разборные с арабскими цифрами цвет серебро diy сделай сам Art Clock 3d зеркальные

На складе в г. Киев

Доставка по Украине

528 грн

Купить

Langeron

Настенные объемные 3D часы разборные с арабскими цифрами цвет черный diy сделай сам Art Clock 3d глянцевые

На складе в г. Киев

Доставка по Украине

528 грн

Купить

Langeron

Настенные объемные 3D часы разборные большие и маленькие арабские цифры + круги цвет серебро diy сделай сам

На складе в г. Киев

Доставка по Украине

528 грн

Купить

Langeron

Настенные объемные 3D часы разборные большие и маленькие арабские цифры + круги цвет черный diy сделай сам Art

На складе в г. Киев

Доставка по Украине

528 грн

Купить

Langeron

Детские часы наручные яркие, объемные, цветная цифра Biaoma Самолет

Доставка по Украине

525 грн

Купить

Superiority

Объемная декоративная цифра 5 стилизованная до Нового года со снижинками из пенопласта Manific Decor

Доставка по Украине

2 270 грн

Купить

Manific Decor

Объемная декоративная цифра 5 стилизованная к Новому году со снежинками из пенопласта

Доставка по Украине

2 770 грн/комплект

Купить

Manific Decor

Объемные 3Д 3D настенные часы с полудрагоценными камнями из эпоксидной смолы на стену зеркальные тихие

Под заказ

Доставка по Украине

3 500 грн

Купить

RESIN.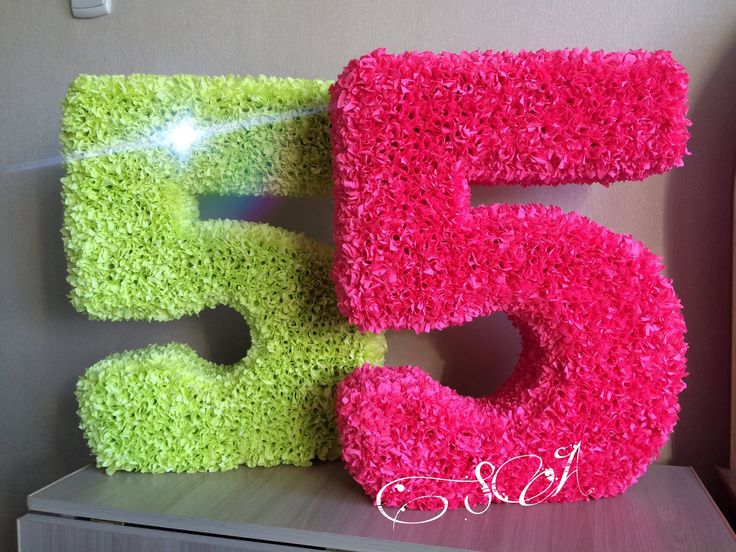 HAUSE.UA

Объемные 3Д 3D настенные часы с полудрагоценными камнями из эпоксидной смолы на стену зеркальные тихие

Под заказ

Доставка по Украине

2 900 грн

Купить

RESIN.HAUSE.UA

Объемные 3Д 3D настенные часы с камнями из эпоксидной смолы на стену зеркальные тихие

Под заказ

Доставка по Украине

3 200 грн

Купить

RESIN.HAUSE.UA

Объемные 3Д 3D настенные часы с полудрагоценными камнями из эпоксидной смолы на стену зеркальные тихие

Под заказ

Доставка по Украине

3 500 грн

Купить

RESIN.HAUSE.UA

Объемные 3Д 3D настенные часы с полудрагоценными камнями коричневие с бежевим эпоксидной смолы на стену тихие

Под заказ

Доставка по Украине

2 900 грн

Купить

RESIN.HAUSE.UA

Свеча Цифра 0 объемная Balloon золото — 1 шт

Доставка по Украине

26 грн

Купить

Интернет — магазин для кондитера

Трехмерные фигуры: определение, площадь и пример

Возможно, вы читаете это перед своим компьютером. Или, может быть, у вас есть стакан воды рядом с вами.

Если вы посмотрите на любой из этих объектов, которые вас окружают, станет ясно, что это объекты в 3D. Но каково математическое определение трехмерной фигуры?

В этой статье мы узнаем больше о трехмерных фигурах и их применении.

Что такое трехмерная фигура?

Трехмерная фигура представляет собой геометрическое тело с тремя пространственными измерениями: длина , ширина и глубина . Иногда глубину называют высотой.

Например, представьте, что вы берете коробку из определенной службы доставки.

Если вы поставите коробку таким образом, что сможете наблюдать только одну из ее граней, вы будете наблюдать плоскую поверхность в 2D, а затем вы будете наблюдать только длину и ширину этой грани.

Но если вы немного повернете его, то увидите, что коробка тоже имеет некоторую глубину. Это то, что мы имеем в виду с трехмерными фигурами.

Как вы могли заметить, глядя на коробку, эти трехмерные фигуры имеют объем . В математике мы определяем объем как количество пространства внутри замкнутой поверхности.

Снова возьмите коробку, и если вы откроете ее сейчас, объем будет равен количеству места внутри коробки. Позже мы узнаем, как вычислить этот объем.

Эти геометрические фигуры обычно, за некоторыми исключениями, которые мы будем использовать, имеют граней , которые являются поверхностями с определенной площадью поверхности, ограничивающими фигуру. Эти лица соединяются в вершин , которые являются точками объединения.

Наконец, линии, ограничивающие эти поверхности и контур геометрической фигуры, называются ребрами . Мы бы сравнили их со сторонами двумерных фигур.

Примеры трехмерных фигур

Отвлекшись от этой статьи и осмотревшись вокруг, вы, вероятно, обнаружите множество трехмерных фигур с различной структурой. От кровати до стула, до стола или даже до книг, которые вы используете для учебы. Все они представляют собой трехмерные фигуры, поскольку они имеют 3 измерения, о которых мы упоминали ранее; длина, ширина и глубина, а также потому, что они имеют объем.

Мы различаем обычные и неправильные трехмерные формы. Мы сосредоточимся на обычных трехмерных фигурах, так как они более распространены в математике.

Конус

Конус — это трехмерная фигура, которую мы получили бы, если бы прямоугольный треугольник (с одним углом, равным 90º) повернулся с фиксированной одной из сторон, таким образом, мы получили бы форму в 3d . Эта фигура обычно имеет круглое основание и вершину , к которой сужается боковая поверхность конуса.

Основание не обязательно должно быть кругом, это может быть и другая двухмерная круглая фигура, например овал. Вы можете наблюдать эту форму в реальном мире, когда смотрите на дорожные конусы.

Пирамида

Эта фигура похожа на конус, но в этом случае основание не имеет круглой формы. Основание представляет собой двухмерную фигуру с тремя или более сторонами, например треугольник, квадрат, прямоугольник и т. д.

Поскольку геометрическая форма основания может варьироваться, изменяется и количество ребер. Все его поверхности, сколько бы их ни было, сужаются к вершине.

Известные египетские пирамиды являются одним из примеров этих геометрических форм, в данном случае они имеют квадратное основание.

Куб

Эта геометрическая фигура состоит из шести равновеликих граней, три из которых сходятся в одной вершине, всего восемь вершин и двенадцать ребер.

Примером куба является игральная кость. Если вы заметите это, все грани обычной игральной кости имеют одинаковую поверхность, и каждая ее вершина работает как объединение трех разных граней.

Прямоугольная призма

Похожа на куб, так как также имеет восемь вершин, двенадцать ребер и шесть граней, но в этом случае не все грани равны. Каждая грань равна своей противоположности, поэтому у нас есть пары равных граней.

Примером прямоугольной призмы может быть ящик или даже коробка, хотя иногда они имеют форму куба.

Существуют и другие виды призм, в зависимости от формы основания и противоположной стороны. Например, если эти грани имеют форму треугольника, это треугольная призма , которая будет иметь всего пять граней вместо шести, как у прямоугольной призмы. Но это основание (и противоположная грань) может иметь другую двумерную фигуру, которая дает различные типы призм: пятиугольные призмы , шестиугольные призмы и т. д.

Цилиндр

Форма этой фигуры может напоминать прямоугольной призмы, но в данном случае она имеет две поверхности, которые называются вершиной и низ (или основание) фигуры, состоящей из двухмерных круглых фигур.

У этой фигуры нет вершины. Поверхность, соединяющая эти две грани, по существу представляет собой прямоугольник, но изогнутый.

Такие геометрические фигуры можно найти в банках или стаканах.

Сфера

Футбол, баскетбол или, может быть, если мы не хотим ограничиваться только спортивным миром: пузырь. Все эти объекты имеют одну общую черту: они являются сферами.

Эти геометрические фигуры получаются, если мы делаем круг, который представляет собой двумерную фигуру, повернутую вокруг своего диаметра. Объем, описываемый этим оборотом, определяется как сфера.

Как и в случае с кругом в двух измерениях, все точки поверхности находятся на одинаковом расстоянии от точки в центре фигуры. Это расстояние называется радиусом . Если мы проследим расстояние между двумя точками поверхности сферы, проходящей через ее центр, то это расстояние называется диаметр сферы, что соответствует удвоенному радиусу.

Формулы трехмерных фигур

При работе с трехмерными фигурами есть некоторые вещи, которые мы могли бы знать о них. В частности, нас интересуют две характеристики.

Первая — это площадь фигуры.

Площадь фигуры – это площадь поверхности, которую занимают грани фигуры. Единицами площади поверхности фигуры являются единицы площади, стандартными являются квадратные метры (м2).

Чтобы получить общую площадь поверхности фигуры, мы должны просуммировать площади каждой грани фигуры. Не следует путать площадь поверхности фигуры с ее объемом. Площадь состоит только из поверхности граней, независимо от того, что находится внутри них.

С другой стороны, у нас есть объем фигуры.

Объем фигуры – это количество пространства внутри поверхности, ограниченной гранями фигуры. Единицами объема являются единицы объема, стандартными являются кубические метры.

Если мы снова возьмем коробку, о которой мы говорили в этой статье, вы увидите, что поверхность картона, используемого для всех граней, соответствует площади поверхности коробки, но пространство внутри коробки соответствует к его объему.

Давайте посмотрим, как выглядят некоторые математические уравнения для трехмерных фигур, которые мы видели раньше.

Площадь и объем конуса

Площадь поверхности трехмерной фигуры равна сумме площадей ее граней.

Для конуса площадь поверхности его основания равна , где r — радиус окружности. Площадь боковой грани равна , будучи г расстояния между любой точкой ребра основания до вершины. Таким образом, площадь поверхности конуса обычно выражается как

.

Объем конуса определяется по следующей формуле:

,

, где h — расстояние от центра основания до вершины.

Площадь и объем пирамиды

В этом случае формулы площади и объема будут зависеть от количества ребер, которые имеет основание.

Например, если пирамида имеет квадратное основание, площадь поверхности пирамиды будет равна сумме площади квадрата и суммы площадей каждого треугольника, соединяющего вершины. В общем, мы можем выразить площадь поверхности пирамиды как

Будьте осторожны, так как основание не обязательно должно быть правильным, и площадь поверхности треугольников, соединяющихся с вершиной, тоже не обязательно должна быть правильной.

Объем пирамиды также зависит от ее основания. Для квадратной пирамиды объем вычисляется по формуле:

равно

Площадь и объем прямоугольной призмы и куба

В этом случае, поскольку прямоугольная призма и куб образованы шестью гранями, для получения общая площадь поверхности фигуры, нам просто нужно суммировать площади каждой грани.

Для куба все шесть граней будут иметь одинаковую площадь, но для прямоугольной призмы, поскольку каждая грань равна своей противоположности, есть три разных значения. Общее математическое выражение для площади поверхности прямоугольной призмы:

где A ₁ , A ₂ и A _{3 являются этими тремя различными областями. Площадь прямоугольника равна.}

Объем этих фигур равен произведению трех ребер; длина, ширина и глубина призмы, например,

В случае куба, поскольку все стороны имеют одинаковую длину, мы имеем

Площадь и объем цилиндра

Цилиндр состоит из двух окружностей, которые являются верхней и нижней частью фигуры, и изогнутого прямоугольника. Следовательно, если площадь круга равна , сумма всех площадей равна

, где h — высота от одной точки основания до точки наверху в том же положении.

Объем цилиндра описывается следующим уравнением:

Площадь и объем сферы

Известная нам сфера представляет собой другой тип геометрической фигуры, так как она не образована объединением разных граней. Вот почему нам нужно математическое выражение для вычисления площади его поверхности:

. А объем сферы определяется по следующей формуле:

.

Примеры задач на трехмерные фигуры

Теперь давайте рассмотрим некоторые примеры задач, с которыми вы можете столкнуться на трехмерных фигурах.

Найдите объем воды, необходимый для заполнения цилиндрического стеклянного стакана высотой 12 см и радиусом 7 см. Брать .

Решение

Используя

, затем

Кохе хочет сделать коническую кепку радиусом 14 см и высотой 20 см для 8 друзей в преддверии своего дня рождения. Какова общая площадь картонной бумаги, чтобы сделать все 8 для своих друзей?

Решение

Сначала найдем общую площадь поверхности одного конического колпачка. Использование

В этом случае g — высота конуса, равная 20 см, а r — 14 см. Следовательно,

Но это всего лишь площадь 1 конуса, вам нужно найти площадь 8 конусов. Таким образом,

Следовательно, Кохе понадобится картон с общей площадью поверхности 11 968 см ² , чтобы успешно изготовить 8 конических крышек для своих друзей перед вечеринкой по случаю его дня рождения.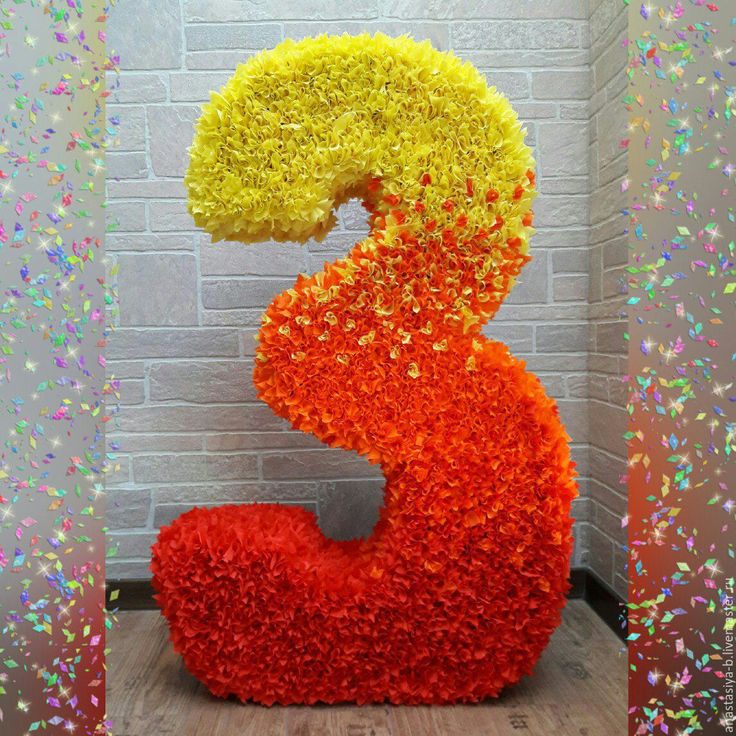

Трехмерные фигуры. Ключевые выводы

• Трехмерные фигуры состоят из трехмерных фигур; длина, ширина и глубина. Иногда глубину называют высотой.
• Эти фигуры имеют образующие их поверхности, называемые гранями. Грани соединяются в вершинах. А линии, ограничивающие эти грани, называются ребрами.
• Существует множество различных примеров трехмерных фигур. Некоторые из наиболее часто используемых фигур — конус, пирамида, куб, призмы, цилиндр и сфера.
• Некоторые трехмерные фигуры, такие как конус, пирамида или сфера, получаются, если заставить двухмерную фигуру вращаться вокруг одной из ее осей или ребер.
• Площадь трехмерной фигуры – это поверхность, занимаемая ее гранями. Как правило, площадь трехмерной фигуры получается путем суммирования площадей всех ее граней. Объем трехмерных фигур — это пространство, которое находится внутри поверхности, ограниченной ее гранями. Чтобы получить его, мы используем различные формулы относительно фигуры, объем которой мы хотим рассчитать.

Как сделать бумажные 3D-фигуры

Изучить математику на практике

• Поделиться

• Твит

Этот пост может содержать партнерские ссылки.

Давайте сделаем объемных фигур из бумаги! Это проще, чем вы думаете.

Меня всегда увлекали оригами и другие поделки из бумаги. Я думаю, что это настолько аккуратно, что из всего лишь листа бумаги можно сделать так много разных вещей. Сегодня я хочу поделиться с вами тем, как мы сделали 6 разных объемных фигур из бумаги. Кроме того, у меня также есть готовые для печати шаблоны для вас.

Научиться делать эти фигуры было бы здорово для геометрии или просто для практики названий трехмерных фигур.

Мои дети думали, что это действительно круто. Некоторое время они играли с ними. Затем они попытались сделать из бумаги множество других фигур. Они были очень очарованы всем этим.

Все, что вам нужно, чтобы сделать эти бумажные 3D-фигуры, это бумага, ножницы, карандаш, линейка и скотч.

У меня также есть шаблоны для печати с еще несколькими трехмерными геометрическими фигурами, если вы хотите сделать их проще! Они доступны в моем магазине.

Есть 6 распространенных трехмерных фигур, о которых я собираюсь рассказать вам сегодня.

• Куб
• Кубовидный (прямоугольный)
• Конус
• Квадратная пирамида
• Треугольная призма (палаткообразная)
• Октаэдр (ромбовидная форма)

Чтобы сделать каждую из этих трехмерных фигур, я использовал лист бумаги размером 8 1/2 x 11.

Как сделать 3D-конус: Для конуса я начертил большой круг, а затем вырезал из него клин. Оберните его и добавьте кусок ленты, чтобы закрепить его.

Как сделать 3D-куб : Для 3D-куба вам нужна крестообразная форма с ровными квадратами. Мои были 2 1/2 дюйма на сторону. Вам нужно четыре квадрата, идущие вниз и три, идущие поперек.

Как сделать трехмерную треугольную призму: Треугольная призма изготавливается путем деления бумаги на трети.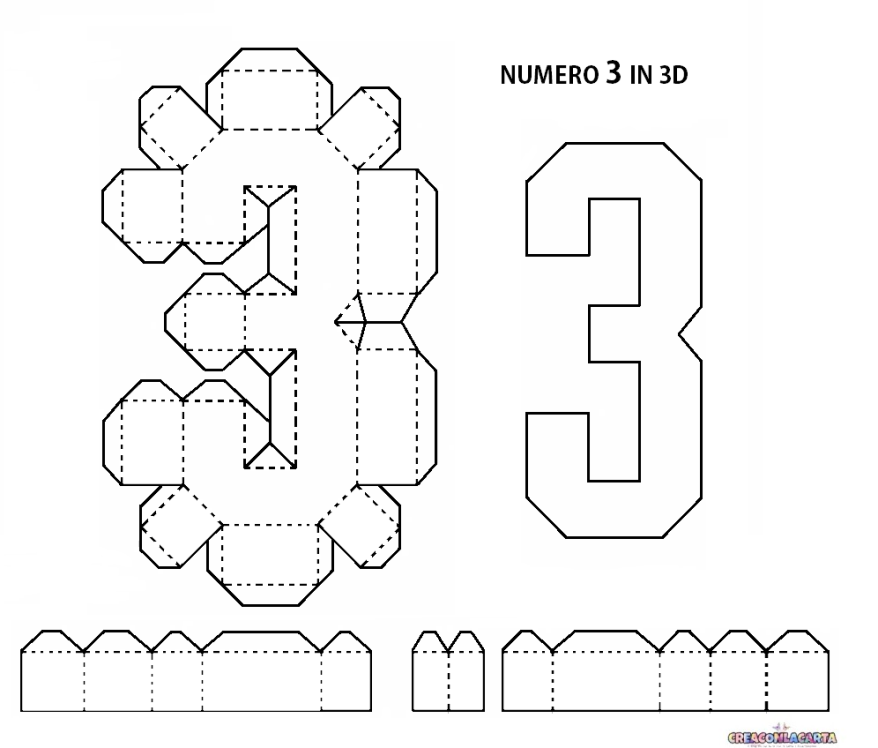 Затем в центральной части сделайте треугольные вырезы. Я измерил стороны своих бумажных секций, чтобы сторона треугольника была одинаковой длины. В итоге получилось 2 3/4 дюйма с каждой стороны.

Как сделать трехмерную пирамиду с квадратным основанием: Пирамида с квадратным основанием начинается с квадрата, а затем с каждой стороны выходят треугольники. У меня около 3 см с каждой стороны. Вы должны убедиться, что каждая сторона треугольника равна сторонам квадрата.

Как сделать 3D кубоид:  Для кубоида я разделил бумагу на четыре части. Затем в одной из секций нужен квадратный вырез. Я сделал это, разрезав другие части и удалив секции.

Как сделать трехмерный октаэдр:   Октаэдр был самым сложным. Это ряд из 8 равносторонних треугольников. Шесть из них стоят в ряд и обращены в противоположные стороны. Два других свисают с концов.

Трехмерный октаэдр Я сделал по 2 дюйма с каждой стороны, но он получился очень маленьким.